오래된 SW 엔지니어의 평생 공부

들어가며

복잡계에 대해서 알게 되면서, 다른 분들께 소개 하기 시작하면서 어떻게 시작하지 고민하게 되었는데요. 돌아가시긴 했지만 당대의 유명한 물리학자라고 할 수 있는 스티븐 호킹 이야기를 안 할 수 없는 것 같습니다. 

" I think the next century will be the century of complexity "
" 나는 다음 세기는 복잡성의 세기가 될 것이라고 생각합니다."

이 분이 20세기 분이기 때문에, 지금 21세기가 복잡계의 세상이 될 것이라는 말씀을 하신거죠. 
이게 상당히 의미 있다고 생각되는게, 물리학자로서 바라보는 흐름을 이야기 하신 것이라 이해합니다. 물리학은 뉴튼 물리학에서 시작해서, 상대성 이론 그리고 양자 물리학을 거쳐서 복잡성 과학에 기초해서 더 발전할 것이라는 기대와 특히, 학제간 연구 (Interdicipline Research)에 복잡성 과학의 적용이 많은 상황으로 이 부분을 언급하는 것이라고 생각합니다.

그런 의미에서도 우리가 복잡계를 알아두고, 혹은 조금이나마 아는척 할 수 있는 정도는 파악하는게 큰 의미 있다 생각이 됩니다.

관련 책소개

우선, 여기서 이야기드릴 내용[1]들은 이런 책들에서 나온 얘기들이에요. 사실 복잡계관련한 책은 더 많지만, 어떤 말씀들을 드릴까 고민을 하면서 항목들을 정리하다가 그 내용이 언급된 책들을 정리하다 보니 총 6권 정도가 되었습니다.

특히 매니지먼트 3.0[2]은 저에게 복잡계라는 주제를 처음 소개한 책입니다. 이 책은 애자일 그 마인드 셋에 기반해서 매니지먼트를 어떻게 할 것인가를 소개하는 책입니다. 즉, 기존의 관리를 이제 1.0 혹은 2.0이라고 하면 이제 애자일 매니지먼트를 3.0이라고 해서 설명하는 책이고, 이 책에서는 다른 애자일 책과는 다르게 이론과 실천법(Practice)들을 번갈아가며 소개하는데요. 여기서 복잡계에 대해서도 다룹니다. 

그리고 전체를 보는 방법[3]도 이제 저희가 제가 이제 처음 거의 처음 복잡계 관련돼서 읽은 책중에 하나인데요. 뒤에 이야기 하겠지만, 집단 지성 혹은 전체주의(Holism)라는 부분에 대해서 소개를 하고 있습니다. 

이제 복잡하지만 단순하게[4] 원제 Simply Complexity 이 책은 정말 잘 쓰여지고 여러 가지 정보를 다루고 있는 책이라고 생각합니다. 여러 분들이 한권만 읽겠다고 하면 이 책을 추천 드릴 것 같습니다. 그렇게 두껍지 않아서 읽는데 부담이 적고, 사례들도 많이 있고 흥미롭게 읽을 수 있을 것 같아서 권해드립니다.

반대로, 스케일[5] 은 굉장히 두꺼운 책이에요. 내가 복잡계 관련해서 좀 책을 봤어 하고 싶은 분은 도전해 보시는 것이 좋겠습니다. 특히, 이 책은 제가 좋아하는 TV 프로그램인 "알쓸신잡"에서도 정승제 교수가 "제프리 웨스트에 의하면..."이라고 이야기 하면서 인용하는 내용이 이책입니다. 간단히 설명하면 복잡계 특징을 가지는 사례들이 규모 변화에 대해서 설명하는 여러 내용이 포함되어 있습니다. 몇 가지 사례를 설명 드릴 겁니다.

링크[6]는 복잡계 네트워크 특히 이제 사람들 관계나 이런 것들에 대해서 기존 다른 네트워크와 복잡계 네트워크에 대해서 설명하고 있는 책입니다. 이를 기반으로 성공에 대해서 분석한 성공의 공식 포뮬라[7] 잠시 소개합니다.

문제를 바라보는 관점으로서의 복잡성

처음 말씀드린 것처럼 매니지먼트 3.0[2]에서 여러 원칙들과 이를 떠받드는 기반 원리에 대해서 설명하는데요. 아래 그림과 같은 마티(Martie)[8]의 오른쪽 다리가 Complexity Thinking입니다. 즉, 복잡성 기반으로 생각하는 것이 중요하다는 것입니다.

매니지먼트 3.0의 저자인 위르헌 아펄로는 구조, 행동 모델[8]을 통해서 문제를 어떻게 바라 보는지 자신만의 설명을 합니다. 행동 쪽에서는 질서(Order), 복잡(Complex), 혼돈(Chaos) 이렇게 나누고 있고,구조는 단순과 난해(Complicated)로 나누어서 설명합니다. 복잡에서 보면, 단순한 구조이면서 복잡한 것은 사람들과의 관계이고, 이것이 난해해지면, 도시 수준이 되는 것이라 볼 수 있습니다.

물론, 다른 유명한 의사 결정 프레임워크로서 커니빈 프레임워크(Cynefin Framework)도 소개합니다. 커네빈은 스코틀랜드 말을 기반으로 해서 스펠링으로 보면 발음에 대해서 알기 어렵습니다. 아는 척 하기 위해서 기억해 두셔야 합니다.

커네빈 프레임워크는 데이브 스노든이 이제 제안하는 의사결정 프레임워크인데 적어놓은 것처럼 관리자들이 상황을 인식하고 이 상황이 어떤 곳에 속하느냐를 인식을 하고 자신 및 사람들의 행동을 이해를 해서 의사결정을 돕기 위한 개념적인 프레임워크라고 할 수 있습니다. 문제를 어디에 포함된 것인지에 따라 다르게 접근하는 것으로 설명합니다. 

여기서 얘기하는 4가지, 분명, 난해, 복잡, 혼돈만 있는 것은 아니고 디스오더라고 해서 여기 어느 곳에도 속하지 않은 상태도 있습니다. 하지만, 여기서 어느 한쪽으로 흘러가게 되어 있습니다. 

분명인 경우에는 베스트 프랙티스를 사용하게 되는데요. 이 때는 문제에 대해서 인식(Sense)하게 되면 어느 Best Practice로 가야할지 분류(Categorize)를 하고 반응(Respond)하면 됩니다. 난해인 경우는 Good Practice로 인식(Sense)를 하게 되면 분석(Analyze)를 해서 실행(Practice)를 하면 됩니다.

복잡(Complex)인 경우는 노블 프렉티스(Novel Practice)라고 완전히 새로운 방법이 필요한 거죠. 그래서 접근하는 방법들이 좀 틀려요. 실험(Probe)하고 인식(Sense)해서 응답(Resond)해야 한다는 접근법을 제안합니다. 

혼돈의 경우는 사고 상황과 같은 것을 고려할 수 있는데요. 이 때는 우선 행동(Action)해야 합니다. 우리가 죽을 수도 있는 상황이니까요. 그리고 나서, 인식(Sense)하고 응답(Respond)합니다. 이런 것들을 나눠서 하자는 게 이제 어떻게 보면 커네빈 프레임워크 그리고 복잡계를 고려한 접근법의 제한 사항이라 볼 수 있습니다.

정의 및 개념

제가 복잡계에 대해서 알게된 상황이나 애자일에 대해 연결된 부분을 이야기 드렸습니다. 그렇다면 도데체 복잡성이란 무엇일까요?

"복잡하지만 단순하게" 나온 얘기인데요, 이런 격언이 있다고 합니다.

"둘이면 좋아도 셋이면 너무 많다."

이 많다는 것이 복잡하다 이런 뜻이기도 한데요. 복잡성 혹은 복잡성 과학의 정의는 "상호작용"을 하는 "개체"들의 집합에서 발생하는 "창발(Emegence)"하는 특징 혹은 그 특징에 대해 연구하는 학문이라고 할 수 있습니다. 여기서, 여기서 상호작용은 이제 피드백 혹은 기억이라고 하고, 창발은 개체들에서 볼 수 없지만 그룹이나 전체로 보면 발견되는 것, 그러한 특징이라 할 수 있습니다. 

크게 어떻게 보면은 또 복잡계는 두 개로 나눠서 설명을 합니다. 하나는 복잡 적응계(Complex Adaptive System, Adaptive Complex Syste) 혹은 복잡 비적응계(Non-adaptive Complex System)이다. 복잡 적응계는 피드백에 다르게 반응하고, 비적응의 경우는 다르게 반응하지 않는 것입니다. 개미와 같은 생명체는 전자이고 싱크대에서 물이 내려가면서 만드는 소용돌이를 후자로 분류합니다.

연구 사례에는 지구 온난화, 교통 체증, 시장 폭락, 바이러스, 암, 전쟁, 테러, 군중, 홍수, 폭염, 태풍, 가뭄, 인터넷 과부하, 대정전 사태가 소개됩니다. 대부분의 상황은 여러 존재들이 식량, 공간, 에너지, 권력, 부 등 "한정된 자원을 놓고 경쟁하는 상황"이 핵심이라고 볼 수 있습니다.

보통 책들에서는 두 가지 다 다루고 있는데 저희가 관심 있는 건 사실은 복잡적응계입니다. 생명체가 있다거나 이런 좀 관련돼 있는 개미 무리 같은 게 그런 게 될 수 있죠.

환원론 vs 전체론

복잡계를 얘기할 때 또 설명하지 않을 수 없는 것 중에 하나가 환원론(Reductionism)과 전체론(Holism)입니다. 

자료[1]에 있는 것 처럼 오리에 대해서 살펴 봅시다. 이 오리를 분해해 보는 거죠. 입이 있고, 식도가 있고 이런 식으로 말입니다. 사실 그렇다면 왼쪽에 있는 것과 살아 있는 오른쪽 오리와 다르지 않을 수 있습니다. 이렇게 보는 것이 환원론입니다.

하지만, 전체론은 오리를 나눠봐도 살아 있는 것이 아니고 이러한 부분이 모여서 살아 있는 오리가 다르다는 것입니다. 이렇 듯, 복잡계에서는 여기서 말씀드린 것처럼 전체론으로 살펴보고 있습니다. 

복잡계로서의 무리(Swarm)

전체를 보는 방법에서 재미있는 것 중에 하나는 복잡계로서의 무리 이 집단 지성에 대해서 다루는 챕터가 있습니다. 사실 흥미로운 비디오[10]를 찾아서 첨부했습니다. 개미와 같은 무리가 지능을 가진 것처럼 움직인다는 예입니다.

개미와같은 경우 여왕개미가 있어가지고 지시하는 대로 움직인다 이렇게 생각할 수 있겠지만 전혀 그렇지 않거든요. 벌 같은 경우도 분봉을 할 때 결국 이제 벌의 무리가 하나로 이렇게 성장을 하다가 다른 쪽으로 나가서 자리를 잡으려고 할 때 장소를 선별하거나 이런 것도 우리가 이제 그것들을 이제 선정을 하고 조사가 되면 중앙의 지시 없이 적절한 장소로 이동해서 나눠집니다.

그리고 벌집의 온도를 조정하는 것도 어떻게 보면 뭐 여왕벌이 더워, 그러니 조절해 이렇게 하는 게 아니고 벌들의 이제 다양한 센서들이 달라서 자기들이 특정한 온도로 이렇게 맞춰져 가게 되는 다양성에 의해서 안정화가 된다는 겁니다. 이런 것들이 단순한 규칙과 피드백들로 이루어 진다는 것입니다.

또 특징적인 것 중에 하나가 이제 자기 조직화 특징이 있습니다. 앞에서도 이야기 한 것 처럼 중앙 통제가 없어요. 자기가 이제 알아서 이렇게 되게 되는 거죠. 그래서 이 비디오를 보시면 어떤 물건을 이제 이상하게 생긴 물건을 이제 옮기는 건데 사람들이 몇 명의 사람들이 같이 움직이는 거 결국 사람들이 생각하는 거 하고 개미들이 이렇게 움직이는 거하고 보여주는 지성이 다르지 않다는 거죠.

최근에 드라마 중에 이제 삼채, 3 body problem도 삼채인이 인간들과 좀 다른 부분이 있는 것 같아요. 삼채인들이 인류를 버그 벌레라고 불렀긴 하지만 결국 그 삼체인들이 좀 굉장히 작은 크기 쌀알 크기라고 알려져 있고 마치 이런 자기들이 실제로 이런 곤충들처럼 굉장히 어려운 각박한 환경에서도 생존하고 인류보다 더 높은 지성을 키워왔던 그런 생명체로서 가능하지 않겠나 이런 생각이 듭니다. 그래서 어떻게 보면 이것이 물론 SF이지만 현실성 있는 가능성 있는 실현성이 있는 상상력이 아닌가 이런 생각이 듭니다. 그래서 이 비디오를 한번 살펴보시면 이 물건들을 옮기는 집단지성 개미들이 보여주는 집단지성에 놀라실 수도 있을 것 같습니다.

복잡계에서의 체계적 크기 변화(Scale) 

이제 스케일[5]에 나온 얘기인데요. 복잡계의 체계적인 규모 변화에 대해서도 설명을 합니다.

그래서 복잡계의 특징으로서는 기본적으로 규모 변화에 대해서는 익스포넨셜(exponential)이다라는 것입니다.  r^k로 이제 설명을 하는데 동물 크기 심장 박동 수 수명 이런 것들을 설명을 합니다. 그래서 실제로 이제 설명할 때 고질라가 실제 같은 크기가 가능하냐 라는 부분에 대해서 증명을 하는데 불가능하다라는 게 이제 그런 부분이에요. 이렇게 보면 이제 포유류로서의 그 크기 심장을 가지고 이렇게 그렇게 그 기관들을 가지면서 할 수 있는 뼈나 이런 것들 지금 가장 큰 크기를 가질 수 있는 포유류는 고래라는 거죠. 대략 34m 이 정도 되는 그런 고래 정도 크기가 최대이고 이거보다 클 수 있는 거는 불가능하다라는 부분에 대해서 또 설명을 하고 있어요.

그리고 도시의 크기와 창의성의 관계 같은 경우도 지수가 아까 여기 보여준 것처럼 약 k가 1.15 정도 보여주는 특징들을 살펴보실 수가 있습니다. 이런 것들이 이제 예로써 스케일이 굉장히 많이 나오는데 재미있는 것 중에 하나가 이 책도 제가 또 흥미롭게 봤던 알쓸신잡의 정재승 박사가 이제 설명할 때 보면 "제프리 웨스트에 의하면.." 이라고 얘기했던 그 부분이 이 스케일에 대해서 언급을 한 부분으로 아실 수가 있습니다.

이것도 굉장히 두꺼운 책이나 사실은 복잡하게 이런 정도 얘기만을 알고 계셔도 아는 척하기에는 딱 적절할 수 있다 이런 생각이 드네요.

복잡계 네트워크

복잡계 얘기를 할 때 복잡계 네트워크를 얘기를 안 할 수가 없을 것 같습니다. 이유 중에 하나는 이제 사람들이 얽혀 있는 네트워크이 그런 거기 때문에 저희가 또 애자이나 이런 쪽에 관심을 가지고 본다고 하면 그 얘기를 하지 않을 수 없고 이 이제 스케일 프리 네트웍크이라는 얘기가 이 스케일이나 링크 이제 성공의 공식 포뮬러[7]에 나옵니다.

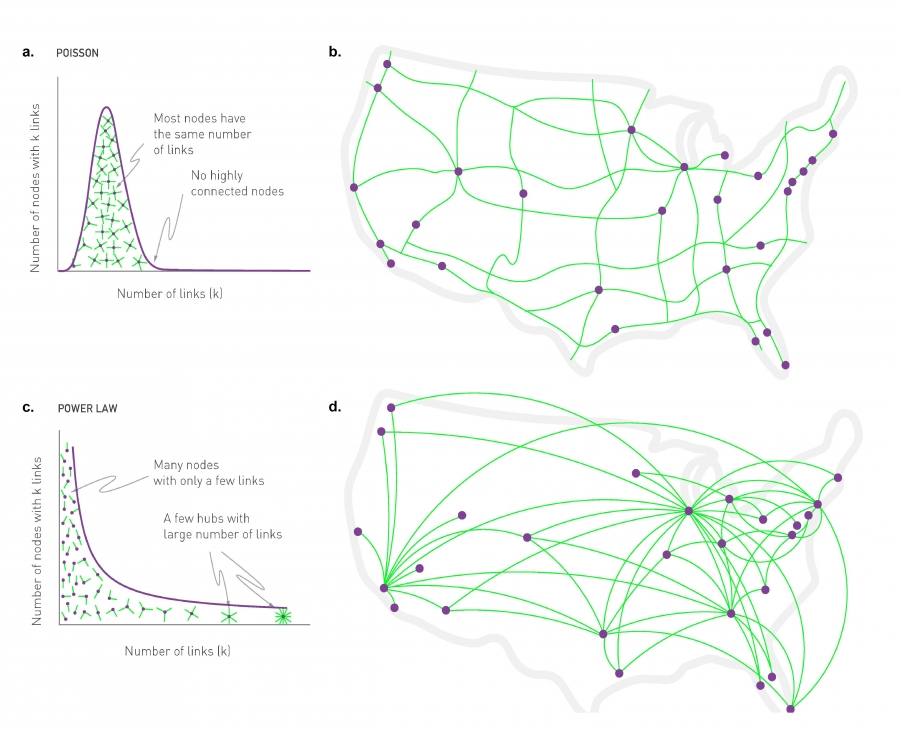
[1]에서 보시는 것처럼 랜덤 네트워크(Randome network)나 이제 스케일 프리 네트워크(Scale-free network)을 비교할 수 있습니다. 스케일 프리 네트워크의 정의를 잘 살펴보면 연결 선의 수의 분포가 멱 법칙을 가집니다.그러니까 결국은 이 연결을 많이 가진 녀석들이 존재해요. 그래서 그걸 허브라고 하는데 이 허브들이 있고 해서, 연결이 끊어 지거나 네트워크가 망가지더라도 회복력이 좋습니다.

그리고, 실제 인간 네트워크이고 보면 좁은 세상 이제 법칙이라고 케빈 베이컨 법칙이라는 게 있습니다. 그래서 여섯 단계에 분리돼 있다. 결국 무슨 얘기냐면 여러분과 이제 몇 단계만 넘어가면 이제 다 안다는 거죠. 쉽게 얘기해서 내가 어떻게 보면은 미국 대통령을 어떻게 알 거냐 라고 하면 내가 아는 분 중에 어떻게 보면 고위 공직자분하고 연결이 돼 있고 그 고위 공직자가 이제 대통령하고 연결돼 있고 대통령이 미국 대통령하고 연결돼 있기 때문에 그런 단계들을 몇 개 넘어가 보면 알기 어려운 분도 연결될 수 있다는 것이죠.

이게 좁은 세상 어떻게 보면 인간 네트워크들이 이렇게 굉장히 좀 작다는 부분이기도 하고 이런 것 때문에 어떻게 보면은 이런 허브들이 많이 가져가게 되기 때문에 승자 독식이라는 부분, 그 다음에 빈익빈 부익부 이런 현상들이 생기는 부분들 그런 것들을 보실 수가 있습니다.

성공의 공식 포뮬라에서도 이제 그런 얘기들을 하는데 여러 법칙들 중에 여기 관련된 것들을 볼 수 있는 것은 1 법칙: 성과는 성공의 원동력이지만 성과를 측정할 수 없을 때는 연결망이 성공의 원동력이 된다 라는 것이죠. 그러니까 결국에 어떻게 연결돼 있는가 누구랑 연결돼 있는가 그런 부분들을 이제 성공의 공식 포뮬러에서 얘기를 하고 있거든요. 그리고, 제 4 법칙 같은 경우는 이제 팀이 성공하려면 다양성과 균형 결국 이제 네트워크들이 튼튼하게 하게 하려는 것이 필요하지만, 팀이 성과를 올리면 오직 단 한 사람만의 공을 독차지한다 이런 얘기가 또 나오게 되어 있습니다.

또 복잡계 네트워크인 스케일 프리 네트워크를 보실 때도 미국 비행기 망이 그런 특징을 가지고 있습니다. 그러니, 허브 공항들이 있습니다. 여기 보면은 아마 LA하고 시카고하고 뉴욕도 보일 겁니다. 

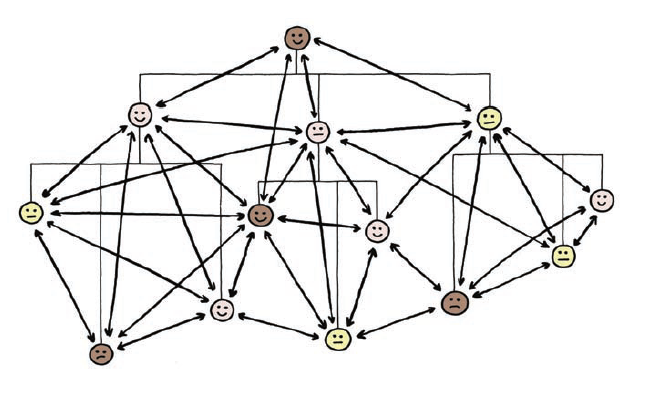
다시, 조직의 네트워크를 살펴 보기 위해, 매니지먼 3.0으로 돌아보면 실제로 이제 권한(Hierarchy)이 존재하지만 네트워크 또 어떻게 보면 좀 다른 걸 수도 있습니다. 이런 상황에서 결국 허브가 되는 사람들이 있다는 것입니다.

마무리

이렇게 복잡계에 대해서 살펴 볼 때에도 사실은 제가 관심 있는 부분인 애자에서 시작해서 보게 됐습니다. 여기 있는 애자일 개발 선언문에서도 여러 가지 부분들을 이제 앞에 설명드렸던 것들을 이해를 할 수 있을 것 같습니다.

결국에는 이제 여기서 강조하는 것도 공정과 도구보다는 개인과 상호작용이 더 중요하다는 부분으 이제 복잡기 안에 있을 때 개인일 수밖에 없고 그거에 대해서 어떻게 보면 더 좋은 저희가 그 복잡한 상황들을 잘 이해하려면 상호작용에 집중해야 한다는 것으로 이해할 수 있습니다.

그리고, 저희가 문서보다는 저희가 작동하는 소프트웨어를 더 강조하는 부분과, 고객이라는 것도 저희 팀으로 본다거나 아니면 환경으로 본다고 하더라도 그 상호작용을 통해서 복잡계로 이해하면 협력을 더 할 수밖에 없는 것이라 생각됩니다.

커네빈 쪽으로 살펴보더라도 아니면 저희가 이제 복잡해서 커니벤 프로임 워크로 문제 해결할 때 대응하는 방식을 하더라도 복잡하다는 상황이라면 결국에는 뭔가 실험하고 거기에 대해서 어댑트 하는 부분들이 필요하다. 결국에는 이제 이런 것들이 저희가 복잡계 과학에서 보듯이 대응하는 방법으로 이제 대응하는 것들을 거기에 활용하는 것들을 복잡기를 가지고 조금 더 이런 것들이 왜 더 중요한지에 대해서 이해할 수 있는 그런 부분이 있기 때문에 어떻게 보면은 애자일과 애자일을 이해하는데 복잡계에 대한 것들이 기본적으로 이해되는 것들이 필요하다고 생각이 되고요.

다시 돌아가서 그런 의미에서 매니지먼트 3.0에서도 어떻게 보면 복잡계를 소개하고 또 매니지먼트 3.0을 바치는 중요한 축으로 설명하는 거라고 생각이 듭니다. 그래서 이 정도만이라도 알고 계셔도  여러 책들을 읽어서 알게 되시는 기본적인 지식들을 아시는 것이라 할 수 있습니다. 그래서, 좀 아는 척하시기 딱 좋지 않을까 이렇게 생각돼서 소개드려봅니다.

참고 도서

[1] 아는척 하기 딱 좋은 복잡계 이야기, https://docs.google.com/presentation/d/1F6EffbTvYQxBiP2gN5dPaSflu3FlC8nOS0JFIRpeGjo/edit#slide=id.g2264d6f5244_0_56
[2] 위르헌 아펄로, "매니지먼트 3.0 - 새로운 시대, 애자일 조직을 위한 새로운 리더십", 에이콘 출판, 조승빈 옮김.
[3] 존 밀러, "전체를 보는 방법 - 박테리아의 행동부터 경제현상까지 복잡계를 지배하는 핵심 원리 10가지", 에이도스, 정형채,최화정 옮김
[4] 닐 존슨, "복잡하지만 단순하게 - 복잡한 세상에도 패턴은 있다", 바다출판사, 한국복잡계학회 옮김
[5] 제프리 웨스트, "스케일 : 생물.도시.기업의 성장과 죽음에 관한 보편 법칙", 김영사, 이한음 옮김

[6] 알버트 라슬로 바라바시, "링크: 21세기를 지배하는 네트워크 과학" 동아시아 

[7] 앨버트 라슬로 바라바시, "성공의 공식 포뮬러", 한국경제신문,  홍지수 옮김
[8] Mamagement 3.0 Foundation Workshop, https://management30.com/workshops/foundation-workshop/
[9] How Complexity Leads to Solutions (Cynefin Framework and the Structure-Behavior Model),  https://management30.com/blog/complexity-solutions-cynefin/
[10] Human vs Ants, https://youtu.be/ZHpu7ngQxwE?si=l7-PLmhJKSi9neR2

배경

제약 이론을 처음 알게 된 것은 데이비드 J. 앤더슨의 칸반 책[1]을 보고 나서였다. 사실 칸반은 도요타 생산 시스템(TPS)의 칸반에서 따온 것이지만 실재로 이론적 배경이 되는 것은 제약 이론이라는 것을 책에서 이야기 한다. 이렇게 발전된 칸반이 TPS의 칸반과 비슷하다는 것을 알게 된 후에 이름을 칸반이라고 붙였다는 일화가 있다. 여기서도 알 수 있 듯이, Lean Thinking과 제약 이론은 일맥 상통하는 부분이 있다고 볼 수 있다. 

제약 이론은 1984년에 처음 책으로 소개되고 2014년의 30주년 기념판[2]이 2019년에 다시 번역되어 나온 엘리 골드렛의 오래된 이론이다. 한마디로 이야기 하면, 시스템의 효율성을 저해하는 제약조건(Constraint)을 찾아내서 극복하기 위한 시스템 개선 방법이라고 할 수 있다.

복잡계를 살펴 보고 있는 지금 조직 혹은 인간 사회, 집단이라는 측면에서 개발팀 혹은 회사라는 것을 복잡계로 볼 때 경영 이론들도 복잡성 과학이라는 측면으로 볼 수 있다. 그렇다면, 제약 이론의 경우는 어떨까? 이 생각으로 이를 정리해 본 것이다.

하이킹 이야기

책[2]의 4막에는 주인공인 알랙스 로저가 토요일 아침 7시에 아들 데이브의 보이스카웃 하이킹에 따라갔다고 우연히 분대장역할을 맏게되고 10마일 떨어진 야영장까지 15명의 아이들을 이끌고 가는 일화를 이야기 하고 있다. 처음 목표는 2마일을 한시간에 가는 정도이면 될 것이라고 목표를 잡았고, 8:30에 출발하여 점심을 한시간 반정도 하고 계속해서 간다면 15:00이면 가능하리라고 보았다.

처음에는 가장 빠른 론이라는 아이를 선두에 두고 일정한 속도로 가게 하였다. 그리고, 아이들에게는 거리가 멀어지지 않게 행진하도록 당부하였다. 하지만, 실재로는 일이 그렇게 쉽게 풀리지 않았다. 중간에 있는 느린 아이의 속도에 뒤에 있던 더 빠른 아이들은 제약을 받았다. 즉, 아무리 빨라도 앞에 있는 아이의 속도에 제약을 받는 것이다. 그렇다고 해서, 아이들의 순서를 바꾼다고 해도 별 소용이 없었다.

이렇게 4시간 정도 걸었어도 실재로 점심시간까지는 겨우 2마일 정도 밖에 가지 못한 것이다. 목표에 대비 한참 부족한 상황이었다. 점심을 먹으며 고민한 알렉스는 균형 잡힌 공장에 대한 시뮬레이션으로 성냥과 주사위로 4명의 아이들과 게임을 하고 하이킹을 하는 15명의 아이들과 자신이 '종속적 사건' 집단이라는 깨닳음을 얻는다.

13:30 다시 출발을 시작하였고, 알랙스는 앞의 사람을 따라 잡기 위해서 열심인 아이들을 보고 자신의 공장도 무언가를 따라잡기 위해 달라고 있었지만 왜 페쇄 직전에 위기에 있는지 고민하기 시작했다. 이런 어려움 속에 5마일 지점에 도착한 일행은 14:30이라는 시간이 된 것을 깨닳는다. 목표로 한 시간과는 30분 밖에 남지 않았다.

이제 반전은 여기서 부터였다. 이때 부터, 일행은 손을 잡고 가면서 앞사람과의 간격을 없앴다. 여기서 가장 속도가 느린 허비라는 친구가 어떻게 하면 빨리 갈 수 있는 방법을 아이들과 찾아 내게 된다. 너무나 많은 짐을 가지고 왔던 허비의 짐을 나눠 가지고 전체의 속도를 높일 수 있었다. 결국은 남아 있던 4마일을 2시간만에 주파하고 17:00에는 캠프장에 도착할 수 있었다.

'종속적 사건'과 전체를 보는 방법.

복잡성 과학에서 꼭 비교 하는 것이 환원 주의(Reductionism)와 전일 주의(Holism)이다. 환원 주의는 부분으로 나누어서 전체를 설명한다는 예전 부터 과학에서 사용되던 통념인데, 복잡성 과학에서는 전체가 부분의 합이 아니라는 전체로 보아야 한다는 관점이다.

하이킹 이야기에서도 하이킹을 하는 아이들을 한명 한명으로 보아서 답이 나오지 않다가, 마지막에는 서로 상호 작용이 타이트하게 일어나도록 손을 잡게 하고 전체적으로 최적화 될 수 있도록 허비의 짐을 나눠 가지게 하면서 최적화가 일어나기 시작한 것을 볼 수 있다.

간단한 사례일지는 모르나, 시스템의 부분 부분을 최적화한다고 해서 전체가 최적화 되지 않는 것은 자주 발견되는 사례이다. 그렇게 때문에 시스템을 전체적(Holistic)하게 보아야 한다. 이 부분이 제약 이론의 복잡성 과학과 연결 되는 부분이라고 생각된다.

균형잡힌 공장(Balanced Plant)와 성장

제약 이론에서는 균현 잡힌 공장에 대해서 이야기 한다. 이는 공장이 시장의 요구 사항에 잘 적응하여 제고가 없이 시장의 요구에 맞게 생산해 내는 공장이다. 하지만, 이것을 목표로 하는 공장은 결국 더 망해 간다고 이야기 한다. 왜 그럴까? 이는 복잡계에서 이야기 하는 성장의 관점으로 볼 수 있다

즉, 성장이 지속 되어야 계속 효율화 되는 것이지 유지 한다면 결국은 성장을 멈추고 죽음의 나락으로 떨어 지는 것을 볼 수 있다. 하이킹 중간에 했던 주사위 게임의 결과도 이를 보여주는 일종의 시뮬레이션이라고 할 수 있다. 그렇다면, 어떻게 하는 것을 책에서는 제안하는 것일까?

하이킹의 예에서는 아이들을 손을 잡게 한다. 이는 종속 사건들을 묶는 것이다. 그리고, 제약 요인을 찾고 이을 전체적으로 효율화 하는 방법을 찾게 하는 것이 접근 방법이었다. 전체적인 시스템에서 종속 사건들이 상호 작용을 하게 거기서 시스템이 효율화 되면서 성장하는 것이다.

성장이라는 측면에서 눈에 보이지 않더라도 이를 계속해야 하는 또 다른 이유가 있다. 이는 붉은 여왕의 달리기 비유에서 살펴 볼 수 있다. 붉은 여왕의 달리기는 루이스 캐럴의 거울 나라의 앨리스에서 붉은 여왕이 앨리스에게 했던 말에서 따온 것인데, "같은 자리를 지키고 있으려면 계속 달리 수 밖에 없다"라는 표현이다. 이는 복잡성 과학을 많이 활용하는 생물학에서는 공진화라는 표현을 쓰는데, 상호 작용하는 여러 종이 환경이 아닌 서로 같이 생존하기 위해서 함께 진화하는 것을 의미한다. 즉, 변화가 없어 보이지만 유지하기 위해서 변화하는 것이다.

최적화 하는 방법.

더 골[2] 책에서는 제약 이론을 정리해서 5단계 시스템을 설명하고 있다.

1단계: 제약 요인을 찾아 낸다.

2단계: 제약 요인을 최대한 이용할 수 있는 방법을 선택한다.

3단계: 다른 모든 공정을 위의 결정에 따라 진행한다.

4단계: 제약 요인을 향상 시킨다.

5단계: 만일 4단계에서 제약 요인이 더 이상 성과를 제약하지 않게 되면 다시 1단계로 돌아간다.

. 경고!: 그러나 관성이 제약 요인이 되지 않도록 주의 한다.

즉, 종속된 사건으로 이루어진 시스템을 최적화 하는 방법을 말하는 것이다. 

복잡계를 설명하는 주요 저서로 볼 수 있는 스케일[3]에서는 여러 이론들을 물리학 및 생물학의 사례를 들어 설명하는 부분이 많다. 최적화 관련해서는 지속적인 다수의 되먹임 및 미세 조정 메커니즘이 자연선택의 진행 과정에 내재해 있고, 그것들이 엄청난 기간에 걸쳐 이루어 지는 것이라고 설명힌다. 더 구체적인 사례가 포유 동물의 심장 출력 최소화가 그것이라고 한다.

여기에 숨어 있는 것이 엄청난 기간이고 이 기간을 구간으로 나누는 것이 생물으 한 세대라고 볼 수 있다. 제약 이론도 반복적인 절차(Iteration)이 일어난다. 생물에서도 한 세대는 부모 세대로 부터 받은 유전자를 통해서 공통된 것도 있고 돌연 변이 유전자도 받게 될 것이다. 환경 혹은 함께 공존하는 종들과 상호 작용을 거치면서 자연 선택의 과정을 거치고 다음 세대로 넘어가는 것이 마치 5단계 시스템에서 일어나는 일과 유사해 보이지 않은가? 

참고 문헌

[1] 데이비드 J. 앤더슨, "칸반: 지속적 개선을 추구하는 소프트웨어 개발," 2014년 11월 30일 출간, 조승빈 옮김, 인사이트

[2] 엘리 골드렛 저, "더 골 The Goal 당신의 목표는 무엇인가?", 동양북스(동양books) 2015년 08월 15일

[3] 제프리 웨스트 저, "스케일 생물, 도시, 기업의 성장과 죽음에 관한 보편 법칙", 김영사, 2018년 07월 30일, 이한음 역